I have played with the idea of implementing an experimental, toy-sized, micro subset of Simulink in javascript for a while. Out of that idea blocksim came to be. It is in no way a candidate for serious numerical simulation, but a simple toy for playing around. It uses Euler’s method for integration, with a configurable step and duration. The user interface was built with Raphaël.js (unrelated to me!) and nv/D3 for plotting.

The idea of this post is to model and simulate a super simple system in both MATLAB and blocksim. I can’t stress this enough: they’re not comparable at all and the point of this post is to simply provide an introduction to blocksim. Let us discuss the following mass-spring-damper system:

The spring with constant $k$ is responsible for a force that is proportional to the displacement $x$ of the mass $m$, and the damper with constant $c$ is responsible for a force that is proportional to its speed, $\dot{x}$. Drawing a free body diagram of the mass $m$, we get:

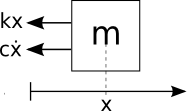
To derive the equation of motion of the center of mass of the block $m$, we may apply Newton’s second law:

\[m\ddot{x} = -c\dot{x} -k\dot{x}\]

That’s it. Once we solve this differential equation for $x(t)$, we will find how the mass $m$ behave in time, given the coefficients $k$ and $c$, as well as its initial position $x(0)$ and speed $\dot{x}(0)$. At this point, you might be thinking “Hey! That’s a homogeneous second-order differential equation with constant coefficients. There are analytical solutions for those! Why do we need to simulate it numericaly”? And you are right: we don’t need to. But there are also reasons to do so:

• We can compare the simulation against the analytical solution for benchmarking;

• Based on experience, we have an idea of how the solution should look like. If you pull a spring in real life, it will want to get back to its resting position, either through an oscillatory movement or a “direct” one.

With our model in hands, we may proceed to write it in a way our software understands. Simulink works in a graphical way using blocks, so our differential equation must be written using those. One very important block is the integrator, which takes a variable as input and outputs its integral. Since our differential equation is a second order one, we may start by using two integrators, since we are interested in finding $x(t)$ given a model with $\ddot{x}(t)$. The finished model looks as follows (with $m=1$ left out for simplicity):

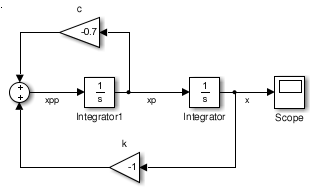
Using blocksim, we arrive at something alike:

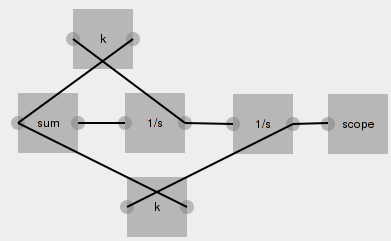
You can toy around with the model here. For simulating, I chose the following parameters:

• $m = 1$
• $k = 1$
• $c = 0.7$
• $x(0) = 2$
• $\dot{x}(0) = 0$
• Simulation length: $20$ seconds
• Integration step: $0.01$ second
• Method: Euler’s

Intuitively, we are interested in finding out what will happen with the mass $m$ if I pull it 2 meters to the right and let it go. Running the simulation, we get the following behavior of $x(t)$ using simulink:

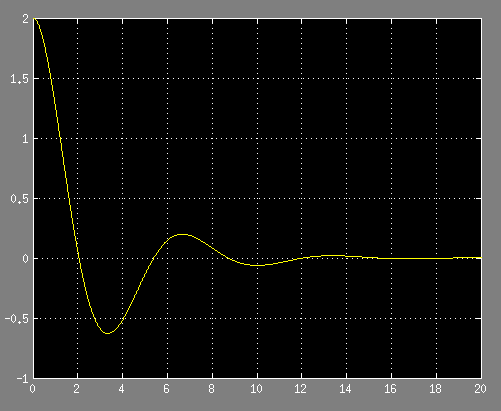
And using blocksim:

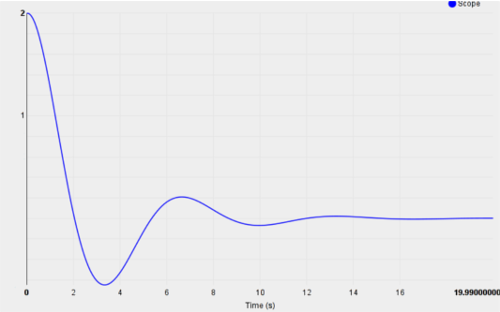
As we might have guessed, this is what happens when we pull the block $m$ 2 meters to the right and let it go: starting at $x(0)=2$, it oscillates around $x = 0$ and the amplitude of the oscillation decreases with time.

Hey! That’s actually pretty cool, isn’t it? Using Euler’s method, a few blocks and a questionable javascript implementation, we were able to get an idea of the system’s behavior. I find it particularly cool to tweak the simulation parameters and see if my intuition matches the simulation output. For example, what would happen if we lower the damping coefficient $c$? Or if we give the mass some inicial speed $\dot{x}(0) \neq 0$? Or if we increase the mass $m$? What is the influence of the integration step?

As said, for such a simple systems, there are analytical solutions that are capable of exactly describing $x(t)$. Numerical simulation are a great tool for simulating more complex systems, as well as nonlinear ones. For instance, if we want to account for dry friction, saturation etc, analytical tools aren’t very useful. Simulations are also useful for designing and testing controllers (maybe on a next post?).

Again, blocksim is not a serious simulation tool and should definitely not be treated as one. In another words, please don’t use it to design your homemade nuclear missile. I hate when it happens.